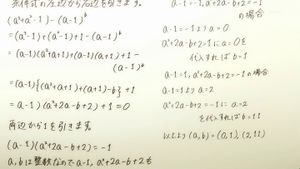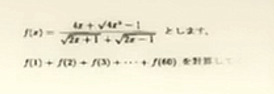Mathematics of Madoka Magica: Difference between revisions
(second solution) |
m (:) |
||
| Line 27: | Line 27: | ||
'''Second Solution''' | '''Second Solution:''' | ||
Homura used in Episode 1 a basic approach with usual integer arithmetic. | Homura used in Episode 1 a basic approach with usual integer arithmetic. | ||
| Line 64: | Line 65: | ||
'''Second solution''' | '''Second solution:''' | ||
The problem can be solved with the binomial theorem: | The problem can be solved with the binomial theorem: | ||
| Line 95: | Line 96: | ||
Find the integer solutions (a,b) with (a^3 + a^2 - 1) - (a - 1)b = 0 | Find the integer solutions (a,b) with (a^3 + a^2 - 1) - (a - 1)b = 0 | ||
'''Solution''' | '''Solution:''' | ||
[[file:Episode One Math S3.jpg|thumb|Episode one Math solution to question 3]] | [[file:Episode One Math S3.jpg|thumb|Episode one Math solution to question 3]] | ||
Revision as of 00:15, 11 March 2011
The cast of Mahou Shoujo Madoka Magica are students of Mitakihara Middle School. Despite merely a middle school, coursework in Mitakihara can be quite challenging. The following are Math problems that have appeared thus far in the show, and their solutions:
Episode 1
Question 1
Any integer divided by 14 will have a remainder between 0 and 13. Given a is has remainder of 6 and b has remainder of 1 when divided by 14, what is the remainder of x when divided by 14, given x is an integer solution to x^2-2ax+b=0?
Solution:
This problem can be solved simply with modular arithmetrics: a = 6 mod 14; b = 1 mod 14; x = r mod 14.
x^2 - 2ax + b = 0 is equivalent to
x^2 - 12x + 1 = 0 mod 14
x(x - 12) = -1 mod 14
-1 has no proper divisors modulo 14, thus factors x and x-12 must correspond to either 1 or -1 mod 14.
If x = 1 mod 14, then x-12 = 3 mod 14: false. If x = -1 mod 14, then x - 12 = 1 mod 14: true.
Therefore, x = -1 mod 14 = 13 mod 14, i.e., the remainder r of x is 13.
Second Solution:
Homura used in Episode 1 a basic approach with usual integer arithmetic.
Let x = 14q + r, a = 14s + 6, b = 14t + 1.
Substitute into x^2 - 2ax + b = 0 to get after some calculations
x^2 - 2ax + b = 14c + (r+1)^2 = 0 with c = 14q^2 + 2q - 28qs - 2rs - 12q + t - r
14 divides 14c and 0, hence it also divides (r+1)^2. This implies that r+1 is divisible by 14.
The question asks for a remainder r between 0 and 13, so we obtain r = 13.
See also: http://green-oval.net/cgi-board.pl/a/thread/44824340
Question 2
Assuming that p is a prime number and n is an arbitrary natural number, prove that (1+n)^p - n^p - 1 is divisible by p.
Solution:
By Fermat's Little theorem, for any prime p and integer a,
a^p = a (mod p)
Thus:
(1+n)^p - n^p - 1 (mod p) is equivalent to
(1+n) - n - 1 (mod p) is equivalent to
0 (mod p)
So the overall expression is divisible by p.
Second solution:
The problem can be solved with the binomial theorem:
For a, b not equal to 0 and nonnegative integer p it holds that:
(a + b)^p = sum (for k from 0 to p) of (p choose k) a^(p-k) b^k where the binomial coefficient (p choose k) is the integer p(p-1)...(p-k+1)/(k(k-1)...1) for 0 <= k <= p
Therefore,
(1 + n)^p = sum (for k from 0 to p) of (p choose k) n^k
and
(1+n)^p - n^p - 1 = sum (for k from 1 to p-1) of (p choose k) n^k
since (p choose 0) = (p choose p) = 1.
It holds that (p choose 1) = p. Since p is a prime number, the factor p in (p choose k) is not divisible by k, k-1,...,2 for 2 <= k <= p-1. Therefore, p divides (p choose k) for 1 <= k <= p-1.
Since each summand on the right side is divisible by p, the whole sum, i.e. the left side is also divisible by p.
Question 3
(Guessing from the solution shown)
Find the integer solutions (a,b) with (a^3 + a^2 - 1) - (a - 1)b = 0
Solution:
(a^3 + a^2 - 1) - (a - 1)b
= (a^3 - 1) + (a^2 - 1) + 1 - (a - 1)b
= (a - 1)(a^2 + a + 1) + (a - 1)(a + 1) + 1 - (a - 1)b
= (a - 1)(a^2 + 2a - b + 2) + 1 = 0
Therefore,
(a - 1)(a^2 + 2a - b + 2) = -1
a, b are integers, therefore the factors a - 1 and a^2 + 2a - b + 2 are integers too. Since the product is -1, one of the factors must be equal to -1, the other to 1.
If a - 1 = -1 then a = 0 and from a^2 + 2a - b + 2 = 1 we obtain b = 1.
If a - 1 = 1 then a = 2 and a^2 + 2a - b + 2 = -1 implies that b = 11.
There are two integer solutions: (a,b) = (0,1) and (a,b) = (2,11).
Question 4
Given File:Math episode one question four.png,
find the sum of F(1)+F(2)+F(3)+...+F(60).
Solution:
Simplying the fraction:
Reference that for any variables a & b, (a-b) (a+b) = (a-b)^2. Let (2x + 1)^.5 = a and (2x - 1)^.5 = b. Multiply F(x) by 1 or (a-b)/(a-b) or ((2x + 1)^.5 - (2x - 1)^.5) / ((2x + 1)^.5 - (2x - 1)^.5). The denominator becomes:
((2x + 1)^.5 + (2x - 1)^.5) * ((2x + 1)^.5 - (2x - 1)^.5)
= (2x + 1) - (2x - 1)
= 2
The numerator becomes:
(4x + (4x^2 - 1)^.5 ) ((2x + 1)^.5 - (2x - 1)^.5)
=(4x + ((2x)^2 - 1)^.5 ) (a - b)
=(4x + (2x - 1)^.5 (2x + 1)^.5 ) (a -b)
=(4x + a b ) (a - b)
=4x (a - b) + (a^2) b - a (b^2)
=4x (a - b) + (2x + 1) b - a (2x - 1)
=4x (a - b) - 2x (a - b) + a + b
=2x ( a - b) + a + b
=(2x + 1) a - (2x - 1) b
=a^3 - b^3
Therefore:
F(x) = (a^3 - b^3 ) / 2
Note that when x= 1, 2, 3, 4, ..., 60;
a^3 = 3^1.5, 5^1.5, 7^1.5, 9^1.5, ..., 119^1.5, 121^1.5;
b^3 = 1^1.5, 3^1.5, 5^1.5, 7^1.5, 9^1.5, ..., 119^1.5;
When summating over F(x) for x between 1 and 60, observe that the majority of the terms in a^3 and b^3 cancel out, leaving:
(121^1.5 - 1^1.5)/2 =((11*11)^1.5 - 1)/2 = 665
Thus, sum of F(x) for x between 1 and 60 is 665. The solution can be generalized as equal to (a(x_max)^3 - b(x_min)^3)/2.
Episode 9
This advanced Algebra problem previously appeared in the first 1992 Tokyo University Entrance Exam:
Problem
A number sequence {F(n)} that can be defined as F(1) = 1, F(2) = 1, F(n+2) = F(n) + F(n+1) (where n is any natural number) is called the Fibonacci sequence and its general solution is given by,
Answer the following questions by using this fact if needed:
Define a sequence of natural numbers X(n) (where n is any natural number), in which each digit is either 0 or 1, set by the following rules:
(i) X(1) = 1
(ii) We define X(n+1) as a natural number, which can be gotten by replacing the digits of X(n) with 1 if the digit is 0, and with 10 if the digit is 1.
For example, X(1) = 1, X(2) = 10, X(3) = 101, X(4) = 10110, X(5) = 10110101, ...
(1) Find A(n), defined as the number of digits of X(n)?
(2) Find B(n),defined as the numbers of times '01' appears in X(n)? For example, B(1) = 0, B(2) = 0, B(3) = 1, B(4) = 1, B(5) = 3,...
Solution
Part 1
Let A(n) equal to the number of digits in X(n), which consists solely of 1s and 0s. Let's suppose x(n) is the number of 0s in X(n) at n iteration (poor choice of variable by the student). Let's suppose y(n) is the number of 1s in X(n) at n iteration.
1) Every time a 0 appears, it is replaced with 1 at the next iteration.
2) Every time a 1 appears, it is replaced with 10 at t he next iteration.
Therefore, the number of 0s in the next iteration is equal to the number of 1s previously:
x(n+1)= y(n)
and the number of 1s in the next iteration is equal to the number of 0s AND the numbers of 1s previously:
y(n+1)=x(n)+y(n)
Prove: x(n) is a fibonacci sequence:
i) y(n+1) = x(n) + y(n)
ii) x(n+2) = y(n+1)
iii) x(n+1) = y(n)
complete the substition shows:
x(n+2) = y(n+1) = x(n) + y(n) = x(n) + x(n+1)
x(n+2) = x(n+1) + x(n) ie definition of fibonacci sequence
Since x(n) is a fibonacci sequence, y(n) is also a fibonacci sequence since x(n+1) = y(n). Therefore:
x(n+2)=x(n+1)+x(n)
y(n+2)=y(n+1)+y(n)
x(n+2)+y(n+2)=x(n+1)+y(n+1)+x(n)+y(n)
Recall: A(n)=x(n)+y(n), therefore
A(n+2)=A(n+1)+A(n)
X(1) = 1, X(2) = 10, X(3) = 101, X(4) = 10110, X(5) = 10110101, ...
therefore: A(1) = 1, A(2) = 2, A(3) = 3, A(4) = 5, A(5) = 8,...
Recall fibonacci sequence F(n): 1, 1, 2, 3, 5, 8. Therefore A(n) = F(n+1), or
Part 2
Let B(n) be the number of times '01' appears in X(n).
Any two digits in X(n) may be 00, 01, 10, 11
the corresponding digits in the next iteration X(n+1) will be
00 -> 11
01 -> 110
10 -> 101
11 -> 1010
Thus, any two digit sequence in X(n) that begins with 1* will contribute to a 01 sequence in the next iteration. In other words, B(n+1) equals y(n), except when unit digit of X(n) is 1, or:
B(n+1) = y(n) - odd(X(n))
y(n) is a fibonacci sequence with starting values: y(1) = 1, y(2) = 1, y(3) = 2 thus y(n) = F(n)
B(n+1) = F(n) - odd(X(n))
B(n) = F(n-1) - odd(X(n-1)), or
Episode 10
Same as Episode One.