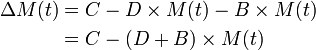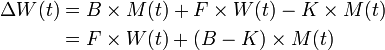Population dynamics
"You know about the food chain, right? I'm sure you learned about it in school. The witches eat the weak humans. And we eat those witches. That's the way stuff works, right?"
-Kyoko in Episode 5
As Kyouko alluded, the relationship between magical girls, witches, and the general population resembles a food chain in nature. However, magical girls and witches shares a unique relationship not typically represented in predator-prey equations: when a magical girl's soul gem darkens completely, she is reborn as a witch (as revealed in Episode 8). This relationship leads to a more complicated interdependence between the two populations, one unaccounted for in standard population modeling. Due to this, a new population model needs to be developed specifically for these magical creatures to properly analyze their population dynamics.
Model assumptions
Both the magical girl and witch populations draw their numbers from the general human population. To simplify calculations, we assume that both populations are many magnitudes smaller in comparison to the overall human population, and human losses that result from magical activities contribute insignificant changes to it.
The magical girl population increases by the number of new girls Kyubey contracted and decreases by the rate of them dying or becoming witches. The Witch population increase by the number of matured familiars per witch as well as the rate of magical girls that became witches, but decreases by the rate magical girls hunt and kill them. We can summarize these premises as the following variables:
- M(t): the number of magical girls at the time t (a natural number)
- W(t): the number of witches at the time t (a natural number)
- C: the number of girls Kyubey contracts at each iteration (a natural number)
- D: the proportion of magical girls dying at each iteration (a percentage)
- B: the proportion of magical girls becoming witches (a percentage)
- K: the proportion of witches killed at each iteration (a percentage)
- F: the number of familiars per witch that mature into witches (a positive rational number)
Simple model
A simple mathematical model was initially proposed (various refinements are defined below). In the simple model, the rate of magical girls dying, becoming witches, and killing witches is assumed to be independent of the witch population. This have an effect of simplifying calculations and provides for a closed-form solution to the differential equations. Under this assumption, the populations can be defined as following:
Simulation
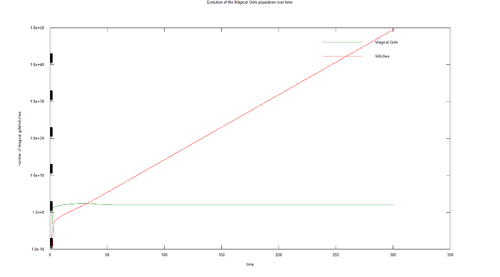
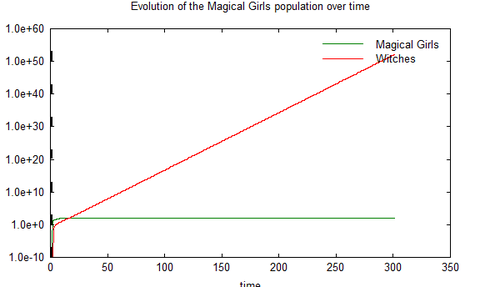
One 100-iterations execution of the simple model with Matlab, using a set of reasonable values for the variables:
| Matlab simulation | Values used |
|---|---|
|
The values used are arbitrary but reasonably selected. Subsequent simulations show that adjustments to the variable values affect curvature but does not affect the general behavior of the populations.
Population at Equilibrium
If both populations are in equilibrium, then there are no changes to either the witch and magical girl population [ΔM(t) = 0 & ΔW(t) = 0]. It follows that the number of magical girls contracted will balance out those that died or become witch in the same period [C = (D + B) M(t)]; and the number of witches matured from minions balances out numbers contributed by magical girls [F * W(t) = (K - B) M(t)].
- At equilibrium, the magical girl population is equal to [math]\displaystyle{ \textstyle{ { C \over {B+D} } } }[/math] .
- At equilibrium, the witch population is (B - K) M(t). If M(t) is also in equilibrium, then the witch population is [math]\displaystyle{ \textstyle{ C \left ( {B-K \over B+D} \right ) } }[/math].
General Solution
The general solution for the witch and magical girl populations in this model are:
for some constant α and β. If we assume witches and magical girls are introduced by QB's civilization, thus initial population of both at the system's introduction were zero [M(0)=0 W(0)=0]. W(t) and M(t) becomes:
Conclusions and observations
- Every dead magical girl is one that did not become a witch. For Kyubey, whose goal is to harvest energy from the magical girl-to-witch transformation, every death meant wasted time contracting the girl. It makes sense for him to design a system where most Witches are weaker than Magical Girls in order to reduce the magical girl casualty rate [K > B].
- If magic girls are stronger than witches, it follows that the typical Magic Girl will kill multiple Witches before becoming one [K - B > 0]. Because of this, there's a need for an alternative source for creating witches. This explains why that despite Kyubey cares only of the energy from Magic Girl-Witches transformation, the supplementary system of witch growth from familiars exist.
- The magical girl population will always reach equilibrium at [math]\displaystyle{ \textstyle{ { C \over {B+D} } } }[/math], regardless of initial number of magical girls or actual values of C, D, or B. The population is limited by Kyubey's ability to contract new girls, and may explain why there seems to be so few magical girls around.
- Even when a significant number of magical girl is introduced initially, their numbers will eventually whithered down to sustainable population level of [math]\displaystyle{ \textstyle{ { C \over {B+D} } } }[/math]. This is a natural consequence of limited by the linear growth rate, independent of any environmental or crowding stresses.
- In contrast, the witch population will never reach equilibrium. The number of witches will fluctuate minutely at the initial period, but inevitably familiar growth will outpace all other factors, and the population will eventually explode into exponential growth. Realistically, the growth may ultimately be capped by human depopulation from witch activities, but at this point the initial premises of the model breaks down.
- Due to the above, any planet with this magical girl and witch system in place is inevitably doomed to extinction. It is not possible to save the human population, with exception of forced extermination of all witches and magical girls. This may explain why in the fourth timeline Kyubey simply chose to abandon Earth rather than attempting sustainable farming of the planet.
Refinements
The simple model provides a mathematical basis for explaining certain idiosyncrasies of the Magica universe, but suffers from overly generalized assumptions that breaks down in some situations. Several refinements were attempted on the simple model to account for these problems. Unfortunately, these refinements need more complex sets of differential equations to properly describe the model, which do not have general solutions and can only be interpreted through simulations.
Witch population dependence
Consider the situation when the magical girls population is substantially bigger than the witch population [M(t) > W(t)]. If there's not many witches around, how do the magical girls find as much opportunity to hunt witches and use magic? Obviously less magic girls will die or become witches, compared to if witches are more abundant. In these situations, the variables [B, K, D] depends not on the current number of magic girls, but on the current number of witches. Based on these premises, ΔM(t) and ΔW(t) may be redefined as:
[math]\displaystyle{ \Delta M(t) = C - (D + B) \times \mathrm{min}(W(t), M(t)) }[/math]
[math]\displaystyle{ \Delta W(t) = F \times W(t) + (B - K) \times \mathrm{min}(W(t), M(t)) }[/math]
where min() chooses the lesser of the two populations.
Simulation
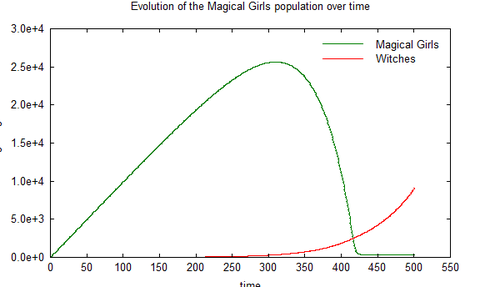
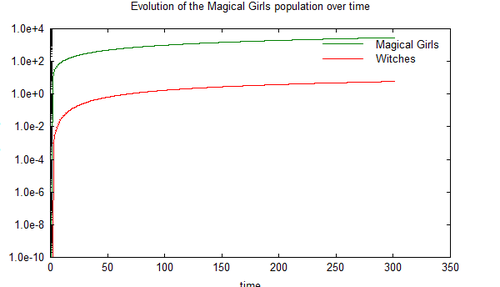
One 500-iterations simulation of this model with Matlab, using a set of reasonable values for the variables:
| Matlab simulation | Values used |
|---|---|
|
Observations
- This model allows for cases where ΔW(t) depends solely on W(t) in low witch population situations, therefore, the initial number of witches must be nonzero. If not, no magical girl would turn into a witch and the witch population is always static at zero. Kyubey may have named this initial witch Walpurgisnaught.
- If F+B-K is less than zero, the number of witches created (be it by magical girls mutation or familiars maturation) is less than the number of witches killed by magical girls. In that scenario, the population of witches [ W(t) ] always extincts rapidly, while magical girls would grow linearly. Additionally, because we previously concluded (from the simple model) that K - B > 0, then F > K - B, implying that more familiars need to mature in each time period than witches killed. To combat this possibility of rapid extinction, witches need to adopt an evolutionary strategy similar to the mass spawning used by most fish and insect species. If sufficient number of familiars bud from each witch, probability of more familiars will mature will increase. This may explain why there are so many familiars in each witch's lair.
- The populations undergo two distinct period of development:
- Initially, the number of magical girls grows in a quasi-linear trend. There are almost no witches, so there are few magical girl casualties. Kyubey still contracts them on a regular basis, so naturally the number grows at a near constant rate. Since less battling occurs, soul gems darken slowly, and the number of magical girls that become witches is comparably smaller. It can be showed that the magical girl population peaks at [math]\displaystyle{ \textstyle{t= { { \ln C - \ln (D+B) } \over {F+B-K} }} }[/math] with maximum population at approximately [math]\displaystyle{ \textstyle{ tC - {C \over {F+B-K} } } }[/math].
- At a critical point where the witch population begin exceeding the magical girl population (around t=300 in this simulation). Increased opportunity of witch hunt starts having an effect on magical girls: magical girl population growth slows then begins to fall, while the witch population increases at an accelerated rate. Eventually the number of magical girls reach equilibrium at [math]\displaystyle{ \textstyle { C \over D+B } }[/math], from this point on the witch population achieves exponential growth.
Comparison with the simple model
The simple model fails to account for this initial period of population development and reach equilibrium at a much faster time. However, the secondary period are comparable to a time-delayed version of the simple model's general solution. Therefore, conclusions reached by the simple model remain valid, although at a later time period than expected by the simple model.
Gradual dimming
While it is not explicitly stated in the show that a Soul Gem gradually dims over time, there are implications for it to be the case. In episode six, we see proof of a constantly active link, of limited range, between a Soul Gem and the body it is linked to. It is reasonable to accept that this link would be magical in nature, and therefore provide a slight but constant drain of the Soul Gem's power. This would allow for Kyubey to start the cycle without an initial number of witches or the possession of a non-canonical ability to directly create a Witch. Let's define a new variable, T, to represent the proportions of magical girls that naturally become witch over time. This changes the model to:
[math]\displaystyle{ \Delta M(t) = C - (D + B) \times \mathrm{min}(W(t), M(t)) - T \times M(t) }[/math]
[math]\displaystyle{ \Delta W(t) = F \times W(t) + (B - K) \times \mathrm{min}(W(t), M(t)) + T \times M(t) }[/math]
Simulation
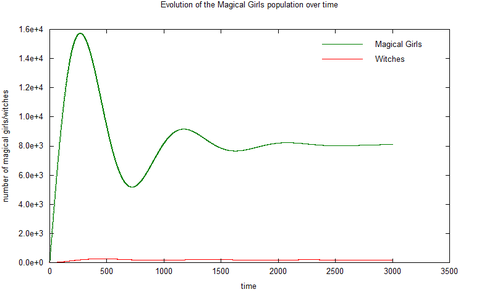
In the case K < B + F, this model's results are similar to the second model. In case K > B + F, the following behaviors can be witnessed:
| Matlab simulation | Values used |
|---|---|
| |
| |
| |
|
Observations
The dynamics of this model depends highly on the variable values and the initial populations used in each simulation:
- In the special case when the witch population never significantly exceed the magical girl population, W(t) and M(t) eventually reach equilibrium when [math]\displaystyle{ \textstyle {W(t)={C \over D+K-F}} }[/math] and [math]\displaystyle{ \textstyle {M(t) = {C \over T} \times {K-F-B \over D+K-F}} }[/math].
- Otherwise the population dynamics will eventually stabilize with M(t) reach equilibrium at [math]\displaystyle{ \textstyle { {C \over D+B+T}} }[/math] and W grows exponentially. This equilibrium is analogous to the general solution of the simple model.
The special case scenario provides a possibility for Kyubey to achieve sustainable farming without destroying the planet, but such a system is incredibly fragile and volatile.
Matlab Scripts
You can find the Matlab scripts for the three models presented above here:
翻訳 (translations)
Some Japanese editions of this article are available.
(この記事には、いくつかの日本語訳があります。)
- 袋小路 個体群動態:翻訳
- 魔法少女まどかマギカ世界の人口変化の考察
- 魔法少女まどか☆マギカにおける魔法少女と魔女の個体群動態 - r_coppeliaの日記 (translated of revision 14:13, 19 March 2011)
The last is translated from revision 14:13, 19 March 2011, that is, without Gradual dimming section.
(最後のものは、2011年3月19日14:13の版から翻訳されています。つまり、ソウルジェムは、なにもしなくても徐々に濁っていくと仮定した場合 の節を含みません。)