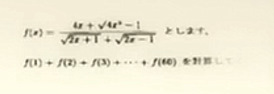Mathematics of Madoka Magica

The following are Math problems and their solutions that has appeared in Madoka Magica.

Episode One

Episode One Math Question 1

Question 1

Any integer divided by 14 will have a remainder between 0 and 13. Given a is has remainder of 6 and b has remainder of 1 when divided by 14, what is the remainder of x when divided by 14, given x is an integer solution to x^2-2ax+b=0?

Solution:

This problem can be solved simply with modular arithmetrics: a = 6 mod 14; b = 1 mod 14; x = r mod 14.

x^2 - 2ax + b = 0 is equivalent to

x^2 - 12x + 1 = 0 mod 14

x(x - 12) = -1 mod 14

-1 has no proper divisors modulo 14, thus factors x and x-12 must correspond to either 1 or -1 mod 14.

If x = 1 mod 14, then x-12 = 3 mod 14: false. If x = -1 mod 14, then x - 12 = 1 mod 14: true.

Therefore, x = -1 mod 14 = 13 mod 14, i.e., the remainder r of x is 13.

Second Solution Homura used in Episode 1 a basic approach with usual integer arithmetic.

Let x = 14q + r, a = 14s + 6, b = 14t + 1.

Substitute into x^2 - 2ax + b = 0 to get after some calculations

x^2 - 2ax + b = 14c + (r+1)^2 = 0 with c = 14q^2 + 2q - 28qs - 2rs - 12q + t - r

14 divides 14c and 0, hence it also divides (r+1)^2. This implies that r+1 is divisible by 14.

The question asks for a remainder r between 0 and 13, so we obtain r = 13.

See also: http://green-oval.net/cgi-board.pl/a/thread/44824340

Question 2

Episode One Math Question 2

(Illegible/need translation)

Question 3

Episode One Math Question 3

(Illegible/need translation)

Question 4

Episode One Math Question 4

Give: File:Math episode one question four.png

Find F(1)+F(2)+F(3)+...+F(60).

Episode Nine

Fibonacci sequence question that appeared in Episode 9

This advanced Algebra problem previously appeared in the 2003 Tokyo entrance exam:

Problem

A number sequence {F(n)} that can be defined as F(1) = 1, F(2) = 1, F(n+2) = F(n) + F(n+1) (where n is any natural number) is called the Fibonacci sequence and its general solution is given by,

Answer the following questions by using this fact if needed:

Define a sequence of natural numbers X(n) (where n is any natural number), in which each digit is either 0 or 1, set by the following rules:

(i) X(1) = 1

(ii) We define X(n+1) as a natural number, which can be gotten by replacing the digits of X(n) with 1 if the digit is 0, and with 10 if the digit is 1.

For example, X(1) = 1, X(2) = 10, X(3) = 101, X(4) = 10110, X(5) = 10110101, ...

(1) Find A(n), defined as the number of digits of X(n)?

(2) Find B(n),defined as the numbers of times '01' appears in X(n)? For example, B(1) = 0, B(2) = 0, B(3) = 1, B(4) = 1, B(5) = 3,...

Solution

Part 1

Let A(n) equal to the number of digits in X(n), which consists solely of 1s and 0s. Let's suppose x(n) is the number of 0s in X(n) at n iteration (poor choice of variable by the student). Let's suppose y(n) is the number of 1s in X(n) at n iteration.

1) Every time a 0 appears, it is replaced with 1 at the next iteration.

2) Every time a 1 appears, it is replaced with 10 at t he next iteration.

Therefore, the number of 0s in the next iteration is equal to the number of 1s previously:

x(n+1)= y(n)

and the number of 1s in the next iteration is equal to the number of 0s AND the numbers of 1s previously:

y(n+1)=x(n)+y(n)

Prove: x(n) is a fibonacci sequence:

i) y(n+1) = x(n) + y(n)

ii) x(n+2) = y(n+1)

iii) x(n+1) = y(n)

complete the substition shows:

x(n+2) = y(n+1) = x(n) + y(n) = x(n) + x(n+1)

x(n+2) = x(n+1) + x(n) ie definition of fibonacci sequence

Since x(n) is a fibonacci sequence, y(n) is also a fibonacci sequence since x(n+1) = y(n). Therefore:

x(n+2)=x(n+1)+x(n)

y(n+2)=y(n+1)+y(n)

x(n+2)+y(n+2)=x(n+1)+y(n+1)+x(n)+y(n)

Recall: A(n)=x(n)+y(n), therefore

A(n+2)=A(n+1)+A(n)

X(1) = 1, X(2) = 10, X(3) = 101, X(4) = 10110, X(5) = 10110101, ...

therefore: A(1) = 1, A(2) = 2, A(3) = 3, A(4) = 5, A(5) = 8,...

Recall fibonacci sequence F(n): 1, 1, 2, 3, 5, 8. Therefore A(n) = F(n+1), or

Part 2

Let B(n) be the number of times '01' appears in X(n).

Any two digits in X(n) may be 00, 01, 10, 11

the corresponding digits in the next iteration X(n+1) will be

00 -> 11

01 -> 110

10 -> 101

11 -> 1010

Thus, any two digit sequence in X(n) that begins with 1* will contribute to a 01 sequence in the next iteration. In other words, B(n+1) equals y(n), except when unit digit of X(n) is 1, or:

B(n+1) = y(n) - odd(X(n))

y(n) is a fibonacci sequence with starting values: y(1) = 1, y(2) = 1, y(3) = 2 thus y(n) = F(n)

B(n+1) = F(n) - odd(X(n))

B(n) = F(n-1) - odd(X(n-1)), or