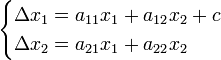Talk:Population dynamics: Difference between revisions
Homerun-chan (talk | contribs) No edit summary |
|||
| Line 64: | Line 64: | ||
It might be nice to investigate it a little, or explain why it is the case if you know... --[[User:Homerun-chan|Homerun-chan]] 17:48, 19 March 2011 (UTC) | It might be nice to investigate it a little, or explain why it is the case if you know... --[[User:Homerun-chan|Homerun-chan]] 17:48, 19 March 2011 (UTC) | ||
:It is a stumbling block I located as well. | |||
:In the case when M(t) > W(t), ΔW=(F+B-K)W, that is, change in witch population depends solely on the current population, modified by the constant (F+B-K). If F+B-K is negative, then ΔW is negative, and the population spirals downwards to zero, and M becomes a linear function Ct. The population dynamics breaks down. The only way to avoid this is if F+B-K is nonegative, but I am not certain how we can justify it, unless we call Kyuubey as a rational agent again. [[User:Prima|Prima]] 17:57, 19 March 2011 (UTC) | |||
Revision as of 17:57, 19 March 2011
refined model analysis
Based off one of my courses, I made a quick analysis of the refined model in terms of convergence and equilibrium. The theorems used are [citation needed] though since they're directly taken from said course's notes (and I only have references for the whole course). Plus I'm not sure the vocabulary is correct in English (translated from french). Please correct it if necessary.
Here goes:
Let's rename the variables for easier notation. x1 will be M(t) and x2 will be W(t). We can generalize the system as follows:
Where a_ij is the contribution of population j to population i (so a12 is the effect witches have on magical girls, etc)
We can write this system using matrix notation:
Where A and C are matrices containing the coefficients. To be exact, let A be
And let C be
File:Population dynamics matrix C.png
The matrix C is constant and hence does not influence the results on stability/equilibrium.
We can prove that (first citation needed), it A's determinant is different than zero, then the only equilibrium for both M(t) and W(t) is when M(0) = 0 and W(0) = 0. (see observations on the page). The determinant of the matrix A is
Let us now discuss the stability, and other equilibria when det A yelds zero (i.e. B=K or D=-B).
Equilibrium
For the further analyses, we ignore Kyubey's contribution (i.e. the matrix C). Basically, adding it would transform an equilibrium into a linear function, and so on.
If det A = 0 (i.e. if (B=K or D=-B), then the only equilibrium is at M(0)=0 and W(0)=0 (no witch, no MG => they can't exist by themselves). Otherwise, [second citation needed], all the equilibria are the states so that
This equation could only be satisfied if D=-B. This is inconsistent with the model (neither the amoung of girls dying nor the amount of girls becoming witches could be negative), so we'll discard this result. Hence, the only equilibrium would be M(0)=0, W(0)=0 when K=B
TODO. Add the stability analysis. I'll do it later but my brain just melt from overheating and speculah overflow.
On a totally unrelated note, >mfw more than 350 tweets about this page in the past hour, and 20-50 more every minute...
- Matrix calculus is not my strong point, so I will need some time to figure out your analysis. In other words, you're right about the tweets: http://mb.tweetbuzz.jp/entry/36044431 . Prima 13:13, 19 March 2011 (UTC)
- I'll try and find the references, that'll make things easier. I'm pretty sure there are a lot of inconsistencies in my analysis too; I don't think ignoring Kyubey's contribution would be so easy... --Homerun-chan 13:16, 19 March 2011 (UTC)
- Ah, the original tweet came from the a Sony developer, Keijiro Takahashi, whom lead the development of Ape Escape 3. Prima 14:09, 19 March 2011 (UTC)
- I see. Too bad we can't put that on our resume ;_; --Homerun-chan 14:28, 19 March 2011 (UTC)
- I see in the refined model, you changed the initial state of W(0) to 1. I think we just found our Walpurgis Night. Prima 17:37, 19 March 2011 (UTC)
Simulations and graphs
I feel that you should add the assumed numbers right above the graphs, because those will affect greatly how the graphs turn out, and I think that putting the numbers up front will enable readers to agree with your starting numbers first.220.255.2.142 13:36, 19 March 2011 (UTC)
- Thanks for the advice, adding it right now. Also, note that they are in the image's description field. --Homerun-chan 13:45, 19 March 2011 (UTC)
Twitter corrections
Along with the other tweets, I found this one that seemed interresting, but I'm not sure I understand it. Basically, they're saying the refined model only works when F+B+1-K>0?
| aibery Original tweet |
Refined modelで魔女が増加するのは F+B+1-K>0 の時だけのような気がするけど、たぶん私が間違ってるんだろう。discussionではmatrixまで用いられてて文系にはちとキツい。 Refined modelで魔女が増加するのは F+B+1-K>0 の時だけのような気がするけど、たぶん私が間違ってるんだろう。discussionではmatrixまで用いられてて文系にはちとキツい。 |
|---|
It might be nice to investigate it a little, or explain why it is the case if you know... --Homerun-chan 17:48, 19 March 2011 (UTC)
- It is a stumbling block I located as well.
- In the case when M(t) > W(t), ΔW=(F+B-K)W, that is, change in witch population depends solely on the current population, modified by the constant (F+B-K). If F+B-K is negative, then ΔW is negative, and the population spirals downwards to zero, and M becomes a linear function Ct. The population dynamics breaks down. The only way to avoid this is if F+B-K is nonegative, but I am not certain how we can justify it, unless we call Kyuubey as a rational agent again. Prima 17:57, 19 March 2011 (UTC)