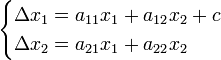Talk:Population dynamics
~~~~) at the end of your comment.refined model analysis
Based off one of my courses, I made a quick analysis of the refined model in terms of convergence and equilibrium. The theorems used are [citation needed] though since they're directly taken from said course's notes (and I only have references for the whole course). Plus I'm not sure the vocabulary is correct in English (translated from french). Please correct it if necessary.
Here goes:
Let's rename the variables for easier notation. x1 will be M(t) and x2 will be W(t). We can generalize the system as follows:
Where a_ij is the contribution of population j to population i (so a12 is the effect witches have on magical girls, etc)
We can write this system using matrix notation:
Where A and C are matrices containing the coefficients. To be exact, let A be
And let C be
File:Population dynamics matrix C.png
The matrix C is constant and hence does not influence the results on stability/equilibrium.
We can prove that (first citation needed), it A's determinant is different than zero, then the only equilibrium for both M(t) and W(t) is when M(0) = 0 and W(0) = 0. (see observations on the page). The determinant of the matrix A is
Let us now discuss the stability, and other equilibria when det A yelds zero (i.e. B=K or D=-B)
TODO. I'll add it but my brain just melt due to overheating. Haven't finished one of the cases and haven't checked that the results are coherent
On a totally unrelated note, >mfw more than 350 tweets about this page in the past hour, and 20-50 more every minute...
- Matrix calculus is not my strong point, so I will need some time to figure out your analysis. In other words, you're right about the tweets: http://mb.tweetbuzz.jp/entry/36044431 . Prima 13:13, 19 March 2011 (UTC)
- Matrix calculus is not my strong point, so I will need some time to figure out your analysis. In other words, you're right about the tweets: http://mb.tweetbuzz.jp/entry/36044431 . Prima 13:13, 19 March 2011 (UTC)