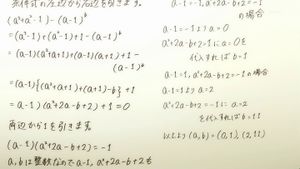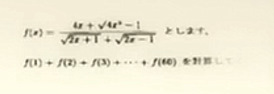Mathematics of Madoka Magica
The cast of Mahou Shoujo Madoka Magica are students of Mitakihara Middle School. Despite merely a middle school, coursework in Mitakihara can be quite challenging. The following are Math problems that have appeared thus far in the show, and their solutions:
Episode 1
Question 1
Any integer divided by 14 will have a remainder between 0 and 13. Given a is has remainder of 6 and b has remainder of 1 when divided by 14, what is the remainder of x when divided by 14, given x is an integer solution to x^2-2ax+b=0?
Solution:
This problem can be solved simply with modular arithmetic:
a = 6 mod 14; b = 1 mod 14; x = r mod 14.
x^2 - 2ax + b = 0 is equivalent to
x^2 - 12x + 1 = 0 mod 14
x(x - 12) = -1 mod 14
-1 has no proper divisors modulo 14, thus factors x and x-12 must correspond to either 1 or -1 mod 14.
If x = 1 mod 14, then x-12 = 3 mod 14: false. If x = -1 mod 14, then x - 12 = 1 mod 14: true.
Therefore, x = -1 mod 14 = 13 mod 14, i.e., the remainder r of x is 13.
Second Solution:
Homura used in Episode 1 a basic approach with usual integer arithmetic.
Let x = 14q + r, a = 14s + 6, b = 14t + 1.
Substitute into x^2 - 2ax + b = 0 to get after some calculations
x^2 - 2ax + b = 14c + (r+1)^2 = 0 with c = 14q^2 + 2q - 28qs - 2rs - 12q + t - r
14 divides 14c and 0, hence it also divides (r+1)^2. This implies that r+1 is divisible by 14.
The question asks for a remainder r between 0 and 13, so we obtain r = 13.
See also: http://green-oval.net/cgi-board.pl/a/thread/44824340
Question 2
Assuming that p is a prime number and n is an arbitrary natural number, prove that (1+n)^p - n^p - 1 is divisible by p.
Solution:
By Fermat's Little Theorem, for any prime p and integer a,
a^p = a (mod p)
Thus:
(1+n)^p - n^p - 1 (mod p) is equivalent to
(1+n) - n - 1 (mod p) is equivalent to
0 (mod p)
So the overall expression is divisible by p.
Second solution:
The problem can be solved with the binomial theorem:
For a, b not equal to 0 and nonnegative integer p it holds that:
where the binomial coefficient (p choose k) is the integer File:Q2 binomial coefficient.png for 0 ≤ k ≤ p.
Therefore,
and
since (p choose 0) = (p choose p) = 1.
It holds that (p choose 1) = p. Since p is a prime number, the factor p in (p choose k) is not divisible by k, k-1,...,2 for 2 ≤ k ≤ p-1. Therefore, p divides (p choose k) for 1 ≤ k ≤ p-1.
Since each summand on the right side is divisible by p, the whole sum, i.e. the left side is also divisible by p.
Question 3
Find the integer solutions (a,b) with (a^3 + a^2 - 1) - (a - 1)b = 0
Solution:
(a^3 + a^2 - 1) - (a - 1)b
= (a^3 - 1) + (a^2 - 1) + 1 - (a - 1)b
= (a - 1)(a^2 + a + 1) + (a - 1)(a + 1) + 1 - (a - 1)b
= (a - 1)(a^2 + 2a - b + 2) + 1 = 0
Therefore,
(a - 1)(a^2 + 2a - b + 2) = -1
a, b are integers, therefore the factors a - 1 and a^2 + 2a - b + 2 are integers too. Since the product is -1, one of the factors must be equal to -1, the other to 1.
If a - 1 = -1 then a = 0 and from a^2 + 2a - b + 2 = 1 we obtain b = 1.
If a - 1 = 1 then a = 2 and a^2 + 2a - b + 2 = -1 implies that b = 11.
There are two integer solutions: (a,b) = (0,1) and (a,b) = (2,11).
Question 4
Given File:Math episode one question four.png,
find the sum of F(1)+F(2)+F(3)+...+F(60).
Solution:
Simplying the fraction:
Reference that for any variables a & b, (a-b) (a+b) = (a-b)^2. Let (2x + 1)^.5 = a and (2x - 1)^.5 = b. Multiply F(x) by 1 or (a-b)/(a-b) or ((2x + 1)^.5 - (2x - 1)^.5) / ((2x + 1)^.5 - (2x - 1)^.5). The denominator becomes:
((2x + 1)^.5 + (2x - 1)^.5) * ((2x + 1)^.5 - (2x - 1)^.5)
= (2x + 1) - (2x - 1)
= 2
The numerator becomes:
(4x + (4x^2 - 1)^.5 ) ((2x + 1)^.5 - (2x - 1)^.5)
=(4x + ((2x)^2 - 1)^.5 ) (a - b)
=(4x + (2x - 1)^.5 (2x + 1)^.5 ) (a -b)
=(4x + a b ) (a - b)
=4x (a - b) + (a^2) b - a (b^2)
=4x (a - b) + (2x + 1) b - a (2x - 1)
=4x (a - b) - 2x (a - b) + a + b
=2x ( a - b) + a + b
=(2x + 1) a - (2x - 1) b
=a^3 - b^3
Therefore:
F(x) = (a^3 - b^3 ) / 2
Note that when x= 1, 2, 3, 4, ..., 60;
a^3 = 3^1.5, 5^1.5, 7^1.5, 9^1.5, ..., 119^1.5, 121^1.5;
b^3 = 1^1.5, 3^1.5, 5^1.5, 7^1.5, 9^1.5, ..., 119^1.5;
When summating over F(x) for x between 1 and 60, observe that the majority of the terms in a^3 and b^3 cancel out, leaving:
(121^1.5 - 1^1.5)/2 =((11*11)^1.5 - 1)/2 = 665
Thus, sum of F(x) for x between 1 and 60 is 665. The solution can be generalized as equal to (a(x_max)^3 - b(x_min)^3)/2.
Episode 8
Homura triangulated the likely location of Walpurgis Night to be the clock tower using Statistics, a branch of Mathematics that determines the probably of a future event by analyzing collective data of similar events.
Episode 9
This advanced Algebra problem previously appeared in the first Tokyo University 1992 Entrance Exam:
Problem
A number sequence {F(n)} that can be defined as F(1) = 1, F(2) = 1, F(n+2) = F(n) + F(n+1) (where n is any natural number) is called the Fibonacci sequence and its general solution is given by,
Answer the following questions by using this fact if needed:
Define a sequence of natural numbers X(n) (where n is any natural number), in which each digit is either 0 or 1, set by the following rules:
(i) X(1) = 1
(ii) We define X(n+1) as a natural number, which can be gotten by replacing the digits of X(n) with 1 if the digit is 0, and with 10 if the digit is 1.
For example, X(1) = 1, X(2) = 10, X(3) = 101, X(4) = 10110, X(5) = 10110101, ...
Anecdote: X(n) can be considered a clever analogy to the show, where Episode 10 should replaces Episode 1 and Episode 1 replaces Episode 0 in the viewer's next viewing.
(1) Find A(n), defined as the number of digits of X(n)?
(2) Find B(n),defined as the numbers of times '01' appears in X(n)? For example, B(1) = 0, B(2) = 0, B(3) = 1, B(4) = 1, B(5) = 3,...
Solution
Part 1
Let A(n) equal to the number of digits in X(n), which consists solely of 1s and 0s. Let's suppose x(n) is the number of 0s in X(n) at n iteration (poor choice of variable by the student). Let's suppose y(n) is the number of 1s in X(n) at n iteration, then x(n) + y(n) = A(n). Since
- Every time a 0 appears, it is replaced with 1 at the next iteration, contributing to a single 1 in X(n+1).
- Every time a 1 appears, it is replaced with 10 at t he next iteration, contributing to a single 1 and a single 0 in X(n+1).
it follows that the number of 0s in the next iteration is equal to the number of 1s previously:
x(n+1)= y(n) ;
and the number of 1s in the next iteration is equal to the number of 0s AND the numbers of 1s previously:
y(n+1)=x(n)+y(n) .
Next, prove that x(n) is a fibonacci sequence, since we know that:
- y(n+1) = x(n) + y(n) ;
- x(n+2) = y(n+1) ;
- x(n+1) = y(n) ;
by substition we can show,
x(n+2) = y(n+1) = x(n) + y(n) = x(n) + x(n+1)
x(n+2) = x(n+1) + x(n)
x(n) fits the definition of a fibonacci sequence. Since x(n) is a fibonacci sequence, it follows that y(n) is also a fibonacci sequence (since x(n+1) = y(n)). Therefore:
x(n+2)=x(n+1)+x(n)
y(n+2)=y(n+1)+y(n)
x(n+2)+y(n+2)=x(n+1)+y(n+1)+x(n)+y(n)
Recall: A(n)=x(n)+y(n), therefore
A(n+2)=A(n+1)+A(n) .
Since, X(1) = 1, X(2) = 10, X(3) = 101, X(4) = 10110, X(5) = 10110101, ...
It follows that A(1) = 1, A(2) = 2, A(3) = 3, A(4) = 5, A(5) = 8,...
Recall fibonacci sequence F(n)= {1, 1, 2, 3, 5, 8, ...}. Therefore A(n) = F(n+1), or
Part 2
Let B(n) be the number of times '01' appears in X(n). Any two digits in X(n) may be 00, 01, 10, 11, and the corresponding digits in the next iteration X(n+1) will be
- 00 -> 11
- 01 -> 110
- 10 -> 101
- 11 -> 1010
Thus, any two digit sequence in X(n) that begins with 1* will contribute to a 01 sequence in the next iteration. In other words, B(n+1) equals y(n), except when unit digit of X(n) is 1, or:
B(n+1) = y(n) - odd(X(n))
where
- odd(n) = 1 if n is odd (unit digit is 1)
- odd(n) = 0 if n is even (unit digit is 0)
y(n) is a fibonacci sequence with starting values: y(1) = 1, y(2) = 1, y(3) = 2 thus y(n) = F(n)
B(n+1) = F(n) - odd(X(n))
B(n) = F(n-1) - odd(X(n-1)), or
Episode 10
Same as Episode 1.